Rsa Key Generation Algorithm Explained Simply
RSA (Rivest–Shamir–Adleman) is an algorithm used by modern computers to encrypt and decrypt messages. It is an asymmetric cryptographic algorithm. Asymmetric means that there are two different keys. This is also called public key cryptography, because one of the keys can be given to anyone. The other key must be kept private. I found some examples generating RSA Key Pais with the java KeyPairGenerator. But what I am searching for is a way to use a existing RSA key pair to encrypt/decrypt messages. How to use RSA Keys with password within Java. Ask Question Asked 6 years, 1 month ago. Active 9 months ago. /. String to hold name of the encryption algorithm.
Key generation is the process of generating keys in cryptography. A key is used to encrypt and decrypt whatever data is being encrypted/decrypted. A device or program used to generate keys is called a key generator or keygen. RSA is one of the first public-key cryptosystems and is widely used for secure data transmission. In such a cryptosystem, the encryption key is public and distinct from the decryption key which is kept secret. In RSA, this asymmetry is based on the practical difficulty of factoring the product of two large prime numbers, the 'factoring problem'. The acronym RSA is the initial letters of the. The RSA algorithm involves four steps: key generation, key distribution, encryption and decryption. A basic principle behind RSA is the observation that it is practical to find three very large positive integers e, d and n such that with modular exponentiation for all integers m (with 0 ≤ m. RSA Function Evaluation: A function (F ), that takes as input a point (x ) and a key (k ) and produces either an encrypted result or plaintext, depending on the input and the key. Key Generation The key generation algorithm is the most complex part of RSA. The aim of the key generation algorithm is to generate both the public and the private. Oct 30, 2017 How does public-key cryptography work? What is a private key and a public key? Why is asymmetric encryption different from symmetric encryption? I'll explain all of these in plain English!
Author: Minh Van Nguyen <nguyenminh2@gmail.com>
This tutorial uses Sage to study elementary number theory and the RSApublic key cryptosystem. A number of Sage commands will be presentedthat help us to perform basic number theoretic operations such asgreatest common divisor and Euler’s phi function. We then present theRSA cryptosystem and use Sage’s built-in commands to encrypt anddecrypt data via the RSA algorithm. Note that this tutorial on RSA isfor pedagogy purposes only. For further details on cryptography orthe security of various cryptosystems, consult specialized texts suchas[MenezesEtAl1996],[Stinson2006], and[TrappeWashington2006].
Elementary number theory¶
We first review basic concepts from elementary number theory,including the notion of primes, greatest common divisors, congruencesand Euler’s phi function. The number theoretic concepts and Sagecommands introduced will be referred to in later sections when wepresent the RSA algorithm.
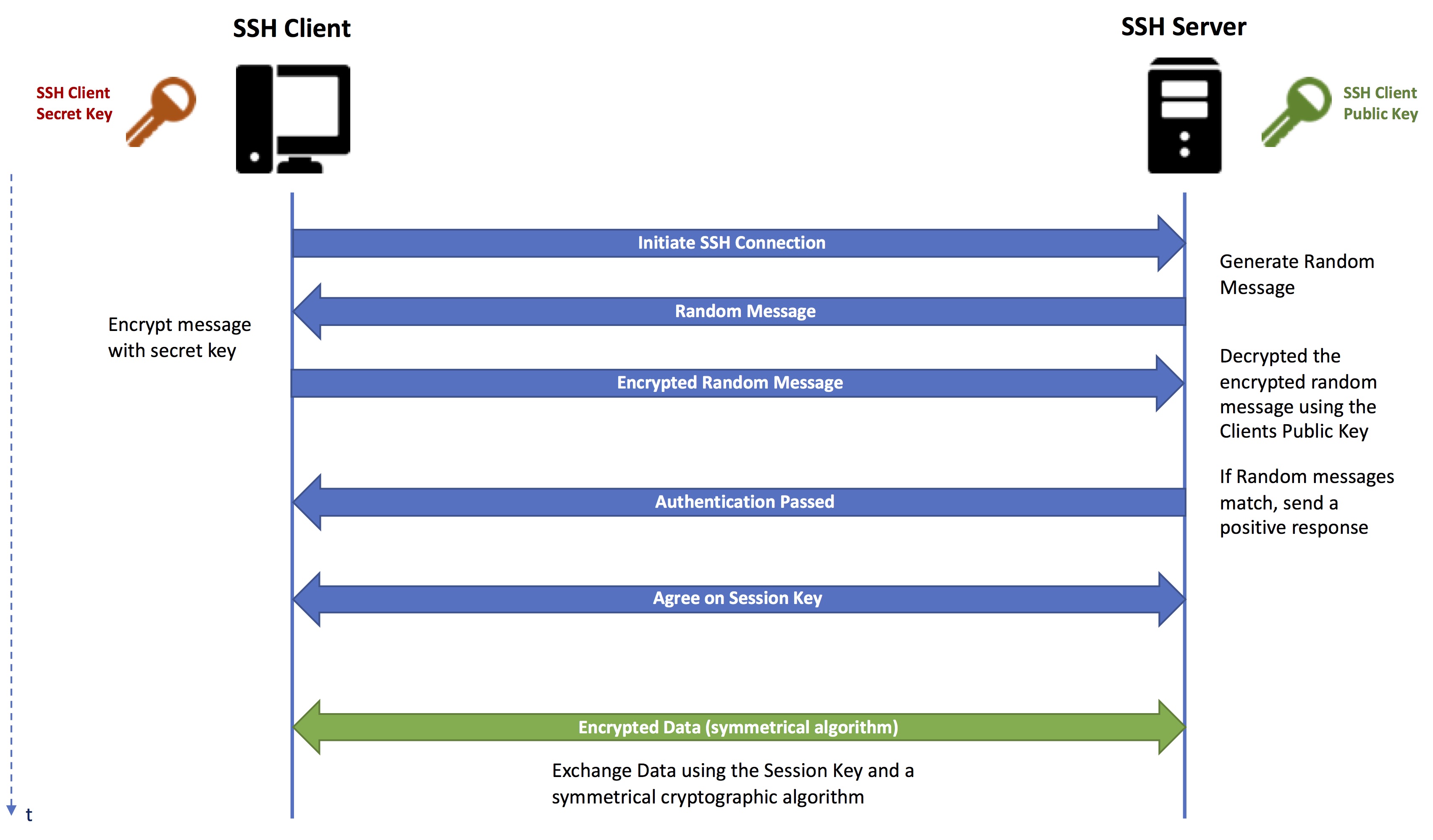
Move your mouse in the area below the progress bar. Open the PuTTYgen program. Click the Generate button. Putty generate key. For Type of key to generate, select SSH-2 RSA.
Prime numbers¶
Public key cryptography uses many fundamental concepts from numbertheory, such as prime numbers and greatest common divisors. Apositive integer (n > 1) is said to be prime if its factors areexclusively 1 and itself. In Sage, we can obtain the first 20 primenumbers using the command primes_first_n:
Greatest common divisors¶
Let (a) and (b) be integers, not both zero. Then the greatest commondivisor (GCD) of (a) and (b) is the largest positive integer which isa factor of both (a) and (b). We use (gcd(a,b)) to denote thislargest positive factor. One can extend this definition by setting(gcd(0,0) = 0). Sage uses gcd(a,b) to denote the GCD of (a)and (b). The GCD of any two distinct primes is 1, and the GCD of 18and 27 is 9.
If (gcd(a,b) = 1), we say that (a) is coprime (or relativelyprime) to (b). In particular, (gcd(3, 59) = 1) so 3 is coprime to 59and vice versa.
Congruences¶
When one integer is divided by a non-zero integer, we usually get aremainder. For example, upon dividing 23 by 5, we get a remainder of3; when 8 is divided by 5, the remainder is again 3. The notion ofcongruence helps us to describe the situation in which two integershave the same remainder upon division by a non-zero integer. Let(a,b,n in ZZ) such that (n neq 0). If (a) and (b) have thesame remainder upon division by (n), then we say that (a) iscongruent to (b) modulo (n) and denote this relationship by
This definition is equivalent to saying that (n) divides thedifference of (a) and (b), i.e. (n ; ; (a - b)). Thus(23 equiv 8 pmod{5}) because when both 23 and 8 are divided by 5, weend up with a remainder of 3. The command mod allows us tocompute such a remainder:
Euler’s phi function¶
Consider all the integers from 1 to 20, inclusive. List all thoseintegers that are coprime to 20. In other words, we want to findthose integers (n), where (1 leq n leq 20), such that(gcd(n,20) = 1). The latter task can be easily accomplished with alittle bit of Sage programming:
The above programming statements can be saved to a text file called,say, /home/mvngu/totient.sage, organizing it as follows to enhancereadability.
We refer to totient.sage as a Sage script, just as one would referto a file containing Python code as a Python script. We use 4 spaceindentations, which is a coding convention in Sage as well as Pythonprogramming, instead of tabs.
The command load can be used to read the file containing ourprogramming statements into Sage and, upon loading the content of thefile, have Sage execute those statements:
From the latter list, there are 8 integers in the closed interval([1, 20]) that are coprime to 20. Without explicitly generating thelist
how can we compute the number of integers in ([1, 20]) that arecoprime to 20? This is where Euler’s phi function comes in handy.Let (n in ZZ) be positive. Then Euler’s phi function counts thenumber of integers (a), with (1 leq a leq n), such that(gcd(a,n) = 1). This number is denoted by (varphi(n)). Euler’s phifunction is sometimes referred to as Euler’s totient function, hencethe name totient.sage for the above Sage script. The commandeuler_phi implements Euler’s phi function. To compute(varphi(20)) without explicitly generating the above list, we proceedas follows:
How to keep a secret?¶
Cryptography is the science (some might say art) of concealingdata. Imagine that we are composing a confidential email tosomeone. Having written the email, we can send it in one of two ways.The first, and usually convenient, way is to simply press the sendbutton and not care about how our email will be delivered. Sending anemail in this manner is similar to writing our confidential message ona postcard and post it without enclosing our postcard inside anenvelope. Anyone who can access our postcard can see our message.On the other hand, before sending our email, we can scramble theconfidential message and then press the send button. Scrambling ourmessage is similar to enclosing our postcard inside an envelope.While not 100% secure, at least we know that anyone wanting to readour postcard has to open the envelope.
In cryptography parlance, our message is called plaintext. Theprocess of scrambling our message is referred to as encryption.After encrypting our message, the scrambled version is calledciphertext. From the ciphertext, we can recover our originalunscrambled message via decryption. The following figureillustrates the processes of encryption and decryption. Acryptosystem is comprised of a pair of related encryption anddecryption processes.
The following table provides a very simple method of scrambling amessage written in English and using only upper case letters,excluding punctuation characters.
Formally, let
be the set of capital letters of the English alphabet. Furthermore,let
be the American Standard Code for Information Interchange (ASCII)encodings of the upper case English letters. Then the above tableexplicitly describes the mapping (f: Sigma longrightarrow Phi).(For those familiar with ASCII, (f) is actually a common process forencoding elements of (Sigma), rather than a cryptographic“scrambling” process per se.) To scramble a message written usingthe alphabet (Sigma), we simply replace each capital letter of themessage with its corresponding ASCII encoding. However, thescrambling process described in the above table provides,cryptographically speaking, very little to no security at all and westrongly discourage its use in practice.
Keeping a secret with two keys¶
The Rivest, Shamir, Adleman (RSA) cryptosystem is an example of apublic key cryptosystem. RSA uses a public key toencrypt messages and decryption is performed using a correspondingprivate key. We can distribute our public keys, but forsecurity reasons we should keep our private keys to ourselves. Theencryption and decryption processes draw upon techniques fromelementary number theory. The algorithm below is adapted from page165 of [TrappeWashington2006]. It outlines the RSA procedure forencryption and decryption.
- Choose two primes (p) and (q) and let (n = pq).
- Let (e in ZZ) be positive such that(gcd big( e, varphi(n) big) = 1).
- Compute a value for (d in ZZ) such that(de equiv 1 pmod{varphi(n)}).
- Our public key is the pair ((n, e)) and our private key is thetriple ((p,q,d)).
- For any non-zero integer (m < n), encrypt (m) using(c equiv m^e pmod{n}).
- Decrypt (c) using (m equiv c^d pmod{n}).
Rsa Key Generation Algorithm Explained Simply 4
The next two sections will step through the RSA algorithm, usingSage to generate public and private keys, and perform encryptionand decryption based on those keys.
Generating public and private keys¶
Positive integers of the form (M_m = 2^m - 1) are calledMersenne numbers. If (p) is prime and (M_p = 2^p - 1) is alsoprime, then (M_p) is called a Mersenne prime. For example, 31is prime and (M_{31} = 2^{31} - 1) is a Mersenne prime, as can beverified using the command is_prime(p). This command returnsTrue if its argument p is precisely a prime number;otherwise it returns False. By definition, a prime must be apositive integer, hence is_prime(-2) returns Falsealthough we know that 2 is prime. Indeed, the number(M_{61} = 2^{61} - 1) is also a Mersenne prime. We can use(M_{31}) and (M_{61}) to work through step 1 in the RSA algorithm:
A word of warning is in order here. In the above code example, thechoice of (p) and (q) as Mersenne primes, and with so many digits farapart from each other, is a very bad choice in terms of cryptographicsecurity. However, we shall use the above chosen numeric values for(p) and (q) for the remainder of this tutorial, always bearing in mindthat they have been chosen for pedagogy purposes only. Refer to[MenezesEtAl1996],[Stinson2006], and[TrappeWashington2006]for in-depth discussions on the security of RSA, or consult otherspecialized texts.
For step 2, we need to find a positive integer that is coprime to(varphi(n)). The set of integers is implemented within the Sagemodule sage.rings.integer_ring. Various operations onintegers can be accessed via the ZZ.* family of functions.For instance, the command ZZ.random_element(n) returns apseudo-random integer uniformly distributed within the closed interval([0, n-1]).
HalfLife Cd-Key'sIm Now adding 20 cd-keys Every day for each gameDay 2-1049-5495-9130-7142-7543-0864-2518-1523-7512-6452-8015-9277-9477-5402-5861-2690-4049-9846-7825-2395-0477-0021-3207-5888-4837-6482-9761-5822-2616-0620-1096-3343-1320-0399-1699-6366-7693-6768-4779-1561-4286-7765-4347-7966-3884-5370-2225-4783-7339-0917-9659-8091-6043-5842-4125-9955-8092-2701-5255-6519-0259-5925-3933-7643-6689-9165-8038-1410-8301-8700Day 2-2866-3096-2039-7865-6746-6031-2730-9429-3227-2407-4054-6143-1816-8804-7733-5811-2733-6011-3936-1245Im Now Adding 20 cd-keys Everyday. Half life key code generator.
We can compute the value (varphi(n)) by calling the sage functioneuler_phi(n), but for arbitrarily large prime numbers (p) and (q),this can take an enormous amount of time. Indeed, the private keycan be quickly deduced from the public key once you know (varphi(n)),so it is an important part of the security of the RSA cryptosystem that(varphi(n)) cannot be computed in a short time, if only (n) is known.On the other hand, if the private key is available, we can compute(varphi(n)=(p-1)(q-1)) in a very short time.
Using a simple programming loop, we can compute therequired value of (e) as follows:
As e is a pseudo-random integer, its numeric value changesafter each execution of e=ZZ.random_element(phi).
To calculate a value for d in step 3 of the RSA algorithm, we usethe extended Euclidean algorithm. By definition of congruence,(de equiv 1 pmod{varphi(n)}) is equivalent to
Rsa Key Generation Example
where (k in ZZ). From steps 1 and 2, we already know the numericvalues of (e) and (varphi(n)). The extended Euclidean algorithmallows us to compute (d) and (-k). In Sage, this can be accomplishedvia the command xgcd. Given two integers (x) and (y),xgcd(x,y) returns a 3-tuple (g,s,t) that satisfiesthe Bézout identity (g = gcd(x,y) = sx + ty). Having computed avalue for d, we then use the commandmod(d*e,phi) to check that d*e is indeed congruentto 1 modulo phi.
Thus, our RSA public key is
and our corresponding private key is

Encryption and decryption¶
Suppose we want to scramble the message HELLOWORLD using RSAencryption. From the above ASCII table, our message maps to integersof the ASCII encodings as given below.
Concatenating all the integers in the last table, our message can berepresented by the integer
There are other more cryptographically secure means for representingour message as an integer. The above process is used fordemonstration purposes only and we strongly discourage its use inpractice. In Sage, we can obtain an integer representation of ourmessage as follows:
To encrypt our message, we raise (m) to the power of (e) and reducethe result modulo (n). The command mod(a^b,n) first computesa^b and then reduces the result modulo n. If the exponentb is a “large” integer, say with more than 20 digits, thenperforming modular exponentiation in this naive manner takes quitesome time. Brute force (or naive) modular exponentiation isinefficient and, when performed using a computer, can quicklyconsume a huge quantity of the computer’s memory or result in overflowmessages. For instance, if we perform naive modular exponentiationusing the command mod(m^e,n), where m, n and e are asgiven above, we would get an error message similar to the following:
There is a trick to efficiently perform modular exponentiation, calledthe method of repeated squaring, cf. page 879 of [CormenEtAl2001].Suppose we want to compute (a^b mod n). First, let(d mathrel{mathop:}= 1) and obtain the binary representation of (b),say ((b_1, b_2, dots, b_k)) where each (b_i in ZZ/2ZZ). For(i mathrel{mathop:}= 1, dots, k), let(d mathrel{mathop:}= d^2 mod n) and if (b_i = 1) then let(d mathrel{mathop:}= da mod n). This algorithm is implemented inthe function power_mod. We now use the function power_mod toencrypt our message:
Thus (c = 630913632577520058415521090) is the ciphertext. To recoverour plaintext, we raise c to the power of d and reduce theresult modulo n. Again, we use modular exponentiation viarepeated squaring in the decryption process:
Notice in the last output that the value 72697676798779827668 is thesame as the integer that represents our original message. Hence wehave recovered our plaintext.
Acknowledgements¶
- 2009-07-25: Ron Evans (Department of Mathematics, UCSD) reporteda typo in the definition of greatest common divisors. The reviseddefinition incorporates his suggestions.
- 2008-11-04: Martin Albrecht (Information Security Group, RoyalHolloway, University of London), John Cremona (MathematicsInstitute, University of Warwick) and William Stein (Department ofMathematics, University of Washington) reviewed this tutorial. Manyof their invaluable suggestions have been incorporated into thisdocument.
Bibliography¶
| [CormenEtAl2001] | T. H. Cormen, C. E. Leiserson, R. L. Rivest, andC. Stein. Introduction to Algorithms. The MIT Press, USA, 2ndedition, 2001. |
| [MenezesEtAl1996] | (1, 2) A. J. Menezes, P. C. van Oorschot, andS. A. Vanstone. Handbook of Applied Cryptography. CRC Press, BocaRaton, FL, USA, 1996. |
| [Stinson2006] | (1, 2) D. R. Stinson. Cryptography: Theory and Practice.Chapman & Hall/CRC, Boca Raton, USA, 3rd edition, 2006. |
| [TrappeWashington2006] | (1, 2, 3) W. Trappe and L. C. Washington. Introductionto Cryptography with Coding Theory. Pearson Prentice Hall, UpperSaddle River, New Jersey, USA, 2nd edition, 2006. |
- Cryptography with Python Tutorial
- Useful Resources
- Selected Reading
RSA algorithm is a public key encryption technique and is considered as the most secure way of encryption. It was invented by Rivest, Shamir and Adleman in year 1978 and hence name RSA algorithm.
Algorithm
The RSA algorithm holds the following features −
RSA algorithm is a popular exponentiation in a finite field over integers including prime numbers.
The integers used by this method are sufficiently large making it difficult to solve.
There are two sets of keys in this algorithm: private key and public key.
You will have to go through the following steps to work on RSA algorithm −
Step 1: Generate the RSA modulus
The initial procedure begins with selection of two prime numbers namely p and q, and then calculating their product N, as shown −
Here, let N be the specified large number.
Step 2: Derived Number (e)
Consider number e as a derived number which should be greater than 1 and less than (p-1) and (q-1). The primary condition will be that there should be no common factor of (p-1) and (q-1) except 1
Step 3: Public key
The specified pair of numbers n and e forms the RSA public key and it is made public.
Step 4: Private Key
Private Key d is calculated from the numbers p, q and e. The mathematical relationship between the numbers is as follows −
The above formula is the basic formula for Extended Euclidean Algorithm, which takes p and q as the input parameters.
Encryption Formula
Consider a sender who sends the plain text message to someone whose public key is (n,e). To encrypt the plain text message in the given scenario, use the following syntax −
Decryption Formula
The decryption process is very straightforward and includes analytics for calculation in a systematic approach. Considering receiver C has the private key d, the result modulus will be calculated as −